Am Himmel sind die Sterne bis auf wenige Ausnahmen selbst mit guten Teleskopen stets punktförmig. Aber ihre Helligkeit ist unterschiedlich. Die Helligkeit ist von der Leuchtkraft \(L\) eines Sternes und von seiner Entfernung vom Beobachter auf der Erde abhängig. Dabei bezeichnet man die Helligkeit, die man auf der Erde empfindet als scheinbare Helligkeit oder scheinbare Größe(nklasse). Ihre Einheit ist die Magnitude oder Magnitudo Die scheinbare Helligkeit ist daher die Helligkeit ohne Berücksichtigung der Sternentfernung.
Einteilung im Altertum
Im Altertum wurden Sterne entsprechend ihrer beobachteten Helligkeit in sechs verschiedene sogenannte Größenklassen eingeteilt. Die 1. Größenklasse beinhaltete besonders helle Fixsterne, die 6. Größenklasse Sterne, die gerade noch mit dem Auge sichtbar sind.
Moderne Festlegung
Heutzutage liegt der Einteilung der Sternenhelligkeit das Weber-Fechner-Gesetz zugrunde. Es besagt im Prinzip, dass für die Stärke \(D\) einer Sinnesempfindung ausgelöst durch einen Reiz der Stärke \(R\) gilt \(D=c\cdot \lg{\frac{R}{R_0}}\). Bei einem exponentiellen Anstieg der Reizstärke wächst die Empfindung im Sinnesorgan nur linear. Dies gilt insbesondere auch für die Wahrnehmung von Helligkeiten durch das menschliche Auge.
Für den Unterschied der scheinbaren Helligkeit \(m\) zweier Objekte in \(\rm{mag}\) (von magnitudo) gilt\[{m_1} - {m_2} = - 2,5 \cdot \lg \left( {\frac{{{E_1}}}{{{E_2}}}} \right)\]wobei \(E\) die Energie pro Zeit und Fläche, also Leistung pro Fläche ist.
Eine umgekehrte Auflösung liefert: \[\frac{{{E_1}}}{{{E_2}}} = {10^{\frac{{{m_2} - {m_1}}}{{2,5}}}} = {\left( {{{10}^{\frac{1}{{2,5}}}}} \right)^{{m_2} - {m_1}}} = {2,51^{{m_2} - {m_1}}}\]
Um hieraus eine einheitliche Skala für die Sternhelligkeit zu gewinnen, ist noch ein fester Referenzwert nötig. Dazu wird klassischerweise der Stern Wega als Nullpunkt gewählt. Seine Helligkeit wird entsprechend mit \(m=0\,\rm{mag}\) festgelegt. Daraus ergeben sich folgende scheinbare Helligkeiten (Magnituden) bzw. Größenklassen:
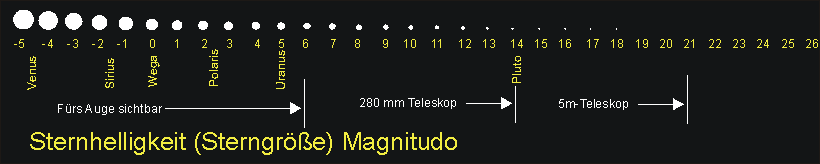
Die Sonne hat eine maximale scheinbare Helligkeit von \(m=-26{,}7\,\rm{mag}\), der Vollmond von maximal \(m=-12{,}7\,\rm{mag}\) und die ISS bei einem geeigneten Überflug maximal \(m=-5\,\rm{mag}\).
Zusammenhang zwischen Größenklassenunterschied und Strahlungsleistungsverhältnis
Aufgrund des logarithmischen Maßstabs entspricht eine gleiche Differenz bei den Helligkeiten (Größenklassen) dem gleichen Verhältnis bei den Strahlungsleistungen.
| Helligkeits-/ Größenklassenunterschied | \({m_2-m_1}\) | \({1}\) | \({2{,}5}\) | \({5}\) | \({7{,}5}\) | \({10}\) | \({12{,}5}\) |
|---|---|---|---|---|---|---|---|
| Leistungs-/Energieverhältnis | \({\frac{E_1}{E_2}}\) | \({2{,}5}\) | \({10}\) | \({100}\) | \({1000}\) | \({10000}\) | \({100000}\) |
Aufgabe
Zwei Sterne haben die scheinbaren Helligkeiten \(6\,\rm{mag}\) und \(1\,\rm{mag}\). Berechnen Sie das Verhältnis ihrer ankommenden Strahlungsleistung pro \({{\rm{m}}^2}\) auf der Erde.
Berechnen Sie, um welchen Faktor sich die Strahlungsleistung pro \({{\rm{m}}^2}\) von Sonne (\(-26{,}7\,\rm{mag}\)) und Vollmond (\(-12{,}5\,\rm{mag}\)) unterscheiden.

