Eine irdische Sonnenfinsternis oder Eklipse (griechisch: ἔκλειψις ékleipsis „Überlagerung, Verdeckung, Auslöschung“) ist ein astronomisches Ereignis, bei dem die Sonne von der Erde aus gesehen durch den Mond ganz (totale Sonnenfinsternis) oder teilweise (partielle Sonnenfinsternis) verdeckt wird.
Eine Sonnenfinsternis kann nur dann Auftreten, wenn sich der Mond in der Neumondphase befindet und sich an einem Schnittpunkt mit der Ekliptikebene von Sonne und Erde befindet.
Ablauf einer totalen Sonnenfinsternis
In der Animation in Abb. 2 kannst du zusammengefasst sehen, wie die Sonnenfinsternis vom 21. August 2017von der Erde aus zu sehen war. Insbesondere die Phase, in der das direkte Sonnenlicht verschwunden ist und nicht mehr alles überstrahlt ist interessant, da dann Leuchterscheinungen zu sehen sind, die sonst vom Strahlungslicht der Sonne überstrahlt werden und nicht sichtbar sind.
Die Animation in Abb. 3 zeigt, wie die Sonnenfinsternis von außen zu sehen wäre. Du kannst sowohl den Kernschatten als kleinen schwarzen Punkt als auch den Halbschatten während des Weges über die Erdoberfläche beobachten.
Beobachter im kleinen Kernschatten beobachten hierbei eine totale Sonnenfinsternis, da der Mond die Sonne vollständig verdeckt. Beobachter im Halbschatten erleben hingegen eine partielle Sonnenfinsternis, da nur ein Teil der Sonne vom Mond verdeckt ist.
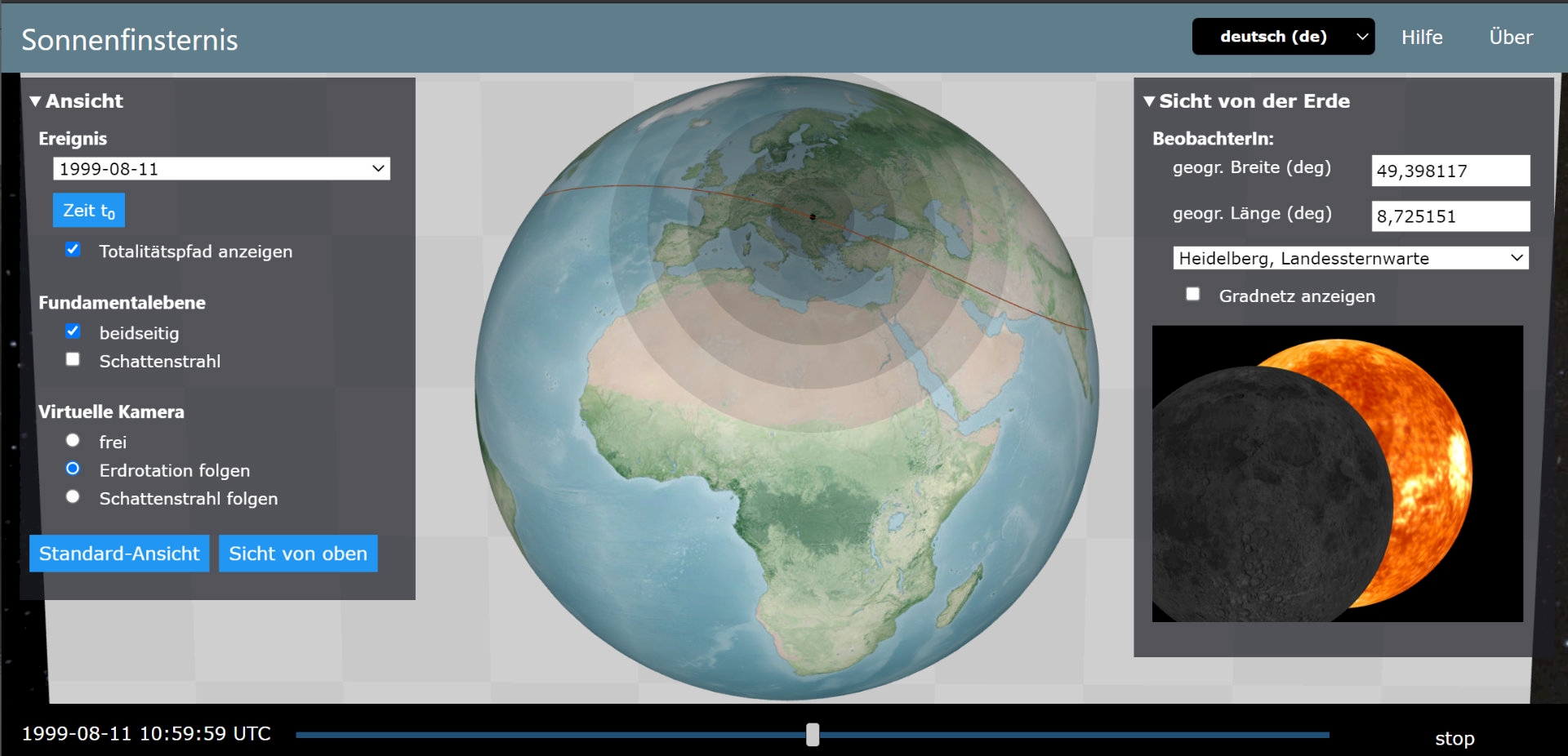
Veranschaulichung in einer Simulation
Das Haus der Astronomie bietet hier die in Abb. 4 gezeigte Simulation zur Veranschaulichung von Sonnenfinsternissen. Darin können verschiedenen Sonnenfinsternisse als Ereignis ausgewählt werden. Im Zentrum wird der Verlauf des Mondschattens über der Erde sichtbar gemacht. Rechts wird der Blick auf die Sonne von einem Beliebige Ort auf der Erde zum gewählten Zeitpunkt dargestellt, sodass der Ablauf der Sonnenfinsternis einfach verfolgt werden kann.
Aufgabe
Gib an, in welcher Mondphase Sonnenfinsternisse zu beobachten sind. Begründe deine Entscheidung.
Gib an, ob man eine Sonnenfinsternis überall auf der Erde gleichzeitig sehen kann, und erkläre deine Aussage.
Erläutere, warum nicht bei jedem Neumond Sonnenfinsternis ist.
Für mathematisch Fortgeschrittene: Der Kernschatten der Erde hat die Form eines geraden Kreiskegels mit der Erdkreisscheibe als Grundfläche. Bekannt sind die folgenden Daten:
| real | verkleinert | |
|---|---|---|
| Sonnendurchmesser \({d_{\rm{S}}}\) | \(1392\cdot10^6\,\rm{m}\) | \(1{,}4\,\rm{m}\) |
| Erddurchmesser \({d_{\rm{E}}}\) | \(12{,}7\cdot10^6\,\rm{m}\) | \(1{,}3\,\rm{cm}\) |
| Monddurchmesser \({d_{\rm{M}}}\) | \(3{,}48\cdot10^6\,\rm{m}\) | \(3{,}5\,\rm{mm}\) |
| Entfernung Erde - Sonne \({d_{\rm{ES}}}\) | \(149600\cdot10^6\,\rm{m}\pm2500\cdot10^6\,\rm{m}\) | \(150\,\rm{m}\) |
| Mittelpunktsentfernung Erde - Mond \({d_{\rm{EM}}}\) | \(384\cdot10^6\,\rm{m}\pm21\cdot10^6\,\rm{m}\) | \(38\,\rm{cm}\) |
Zeige mit Hilfe der obenstehenden Daten durch Rechnung, dass die Länge des Kernschattens \(1378 \cdot {10^6}\,{\rm{m}} \pm 23 \cdot {10^6}\,{\rm{m}}\) beträgt.