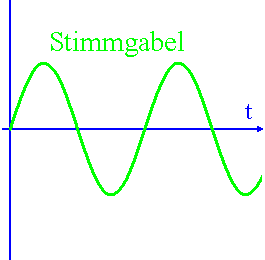
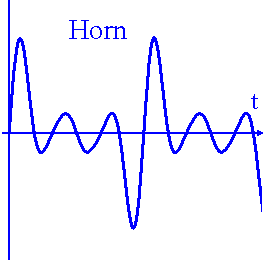
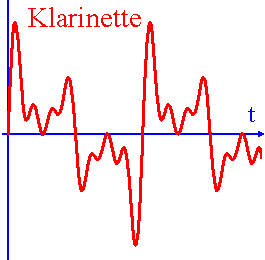
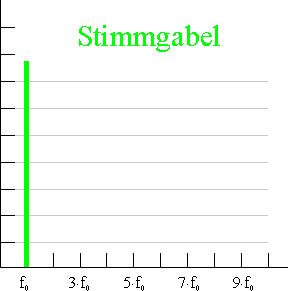Wird ein Ton (z. B. der Kammerton \(\overline{a}= 440\, \mathrm{Hz}\)) mit verschiedenen Instrumenten gespielt, so ist die Klangfarbe deutlich voneinander verschieden. Fachleute erkennen dann auch recht gut, von welchem Instrument der Ton gespielt wurde. Schließt man ein Mikrophon an ein Oszilloskop, so ergeben sich für den Kammerton \( \overline{a} \) gespielt von einer Stimmgabel, einem Horn und einer Klarinette die folgenden Bilder:
 |
 |
 |
 |
 |
 |
Klanguntersuchung durch FOURIER-Analyse
Nach einem Satz des französischen Mathematikers und Physikers Joseph FOURIER (1768 - 1830) kann sich jede noch so komplizierte Eigenschwingung (eines Instruments) auf eindeutige Weise aus harmonischen Eigenschwingungen aufgebaut denken. Das Zerlegen eines periodischen Signals in eine Summe von Sinusfunktionen wird als FOURIER-Analyse bezeichnet.
•Die Analyse des Klangs bei der Stimmgabel zeigt, dass hier nur die Grundschwingung mit der Frequenz \(f_0=440\,\rm{Hz}\) vertreten ist.
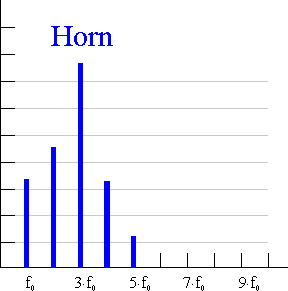
•Bei der Klanganalyse des Horns stellt man neben dem Grundton noch eine Reihe weiterer Obertöne \(f_1=2\cdot f_0\), \(f_2=3\cdot f_0\), \(f_3=4\cdot f_0\) usw., fest. Beim Horn ist insbesondere der zweite Oberton sehr stark vertreten.
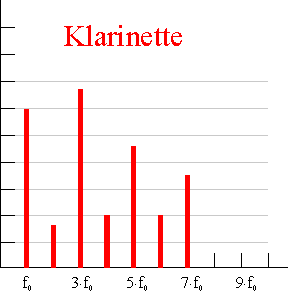
•Auch bei der Klarinette treten zusätzlich zu Grundton eine Reihe von Obertönen auf, wobei hier der 2., 4. und 6. Oberton jeweils stark vertreten ist.
Die obigen Aussagen werden augenfällig im sogenannten Frequenzspektrum dargestellt:
|
|
 |
 |
Hinweis: Will man erkennen, mit welchem Instrument ein Klang gespielt wurde, so ist das Obertonspektrum von großer Bedeutung. Allerdings spielen auch noch andere Merkmale wie z.B. der zeitliche Verlauf der Intensitätsänderungen von Obertönen eine wichtige Rolle.
FOURIER-Synthese
Unter der FOURIER-Synthese versteht man den Aufbau eines periodischen Signals aus Sinusfunktionen. Die Animation in Abb. 3 zeigt den Aufbau des "Horn-Klanges" aus einzelnen Sinustönen.