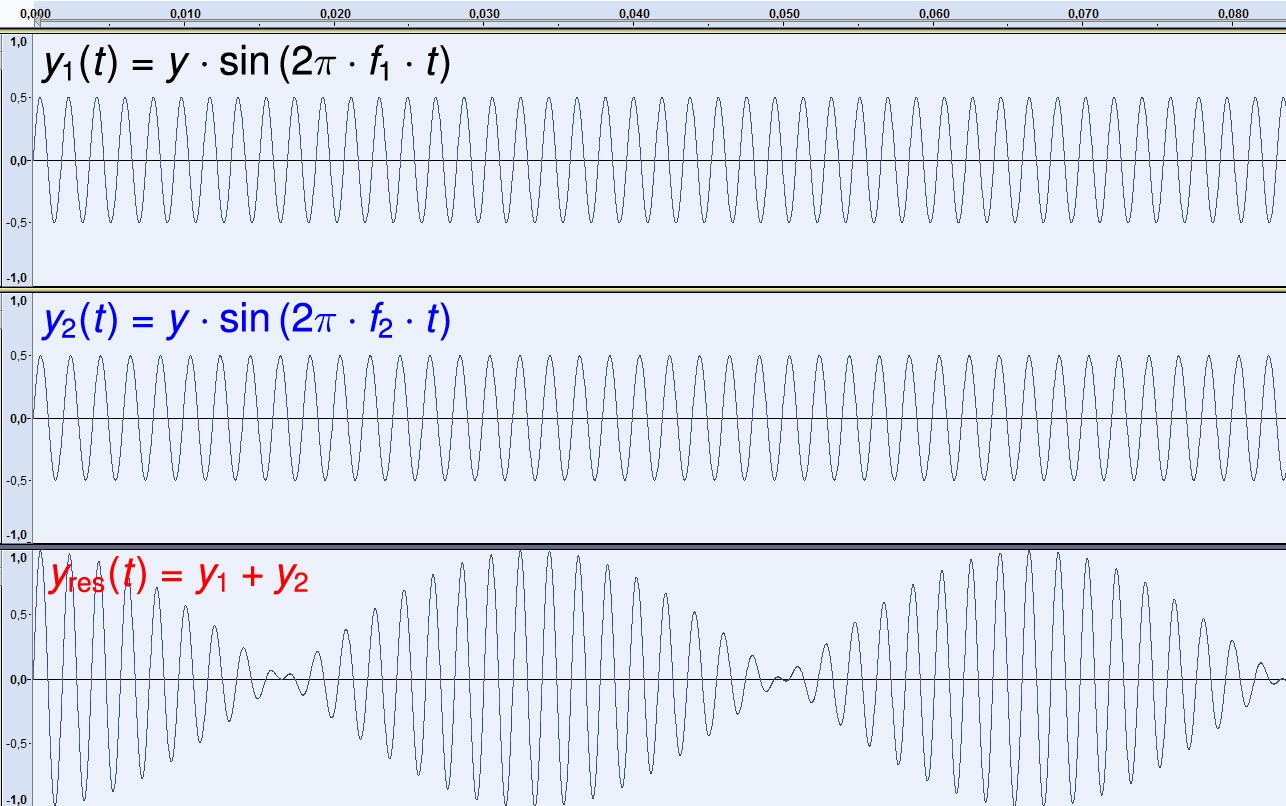
Erzeugt man zwei Töne gleicher Lautstärke (d.h. die Schwingungen haben gleiche Amplitude) mit leicht verschiedenen Frequenzen \({f_1}\) und \({f_2}\) (\({f_1} \approx {f_2}\)), so nimmt unser Ohr nicht die beiden Töne getrennt wahr. Vielmehr hören wir ein An- und Abschwellen eines Tones, dessen Höhe ungefähr mit der Höhe der Ausgangstöne übereinstimmt. Man bezeichnet diese Erscheinung als Schwebung. Die nebenstehende Abbildung zeigt die \(t\)-\(y\)-Diagramme der beiden Ausgangstöne (\(f_1>f_2\) und \({f_1} \approx {f_2}\)). Für die Diagramme wurden \({f_1} = 530\,{\rm{Hz}}\) und \({f_2} = 500\,{\rm{Hz}}\).
Als Überlagerung ergibt sich eine Schwingung (Überlagerungsschwingung), deren Frequenz \({f_{{\rm{R}}}}\) das arithmetische Mittel der beiden Ausgangsfrequenzen ist:\[{f_{{\rm{R}}}} = \frac{{{f_1} + {f_2}}}{2}\]Die Amplitude dieser Überlagerungsschwingung schwankt mit der Frequenz \({f_{{\rm{S}}}}\) (Frequenz der Einhüllenden), für die gilt\[{f_{{\rm{S}}}} = \frac{{{f_1} - {f_2}}}{2}\]Diese Frequenz der Einhüllenden ist in der Regel sehr viel kleiner als die Frequenz der Überlagerungsschwingung \(f_{\rm{R}}\). Als Schwebungsfrequenz bezeichnet man schließlich die Frequenz \({f_{{\rm{Schwebung}}}}\), mit der sich der Betrag der Einhüllenden verändert. Für sie gilt\[{f_{{\rm{Schwebung}}}} = \left| {{f_1} - {f_2}} \right|\]Erklingen nun also zwei Töne, deren Frequenzen sich nur wenig unterscheiden, so ist ein Ton der Frequenz \({f_{{\rm{R}}}}\) zu hören. Dieser Ton ist aber nicht gleich laut, sondern seine Lautstärke schwankt mit der Schwebungsfrequenz \({f_{{\rm{Schwebung}}}}\).
Je näher die beiden Ausgangsfrequenzen beieinander liegen, desto langsamer schwillt die Lautstärke der resultierenden Schwingung an und ab (desto geringer ist die Frequenz der Einhüllenden).
Mathematisch lassen sich die Beziehungen für die resultierende Frequenz und die Schwebungsfrequenz leicht ableiten: Für die resultierende Schwingung gilt: \[{y_{res}}(t) = \hat y \cdot \sin \left( {2 \cdot \pi \cdot {f_1} \cdot t} \right) + \hat y \cdot \sin \left( {2 \cdot \pi \cdot {f_2} \cdot t} \right) \quad(1)\]Aus der Trigonometrie kennt man die folgende Beziehung \[\sin \left( \alpha \right) + \sin \left( \beta \right) = 2 \cdot \sin \left( {\frac{{\alpha + \beta }}{2}} \right) \cdot \cos \left( {\frac{{\alpha - \beta }}{2}} \right) \quad(2)\]Wendet man die Beziehung \((2)\) bei der Gleichung \((1)\) an, so folgt\[\begin{eqnarray}{y_{{\rm{res}}}}(t) &=& \overbrace {2 \cdot \hat y \cdot \cos \left( {2 \cdot \pi \cdot \underbrace {\frac{{{f_1} - {f_2}}}{2}}_{\;{f_{\rm{S}}}} \cdot t} \right)}^{{\rm{Amplitudenfaktor}}} \cdot \sin \left( {2 \cdot \pi \cdot \underbrace {\frac{{{f_1} + {f_2}}}{2}}_{{f_{\rm{R}}}} \cdot t} \right)\\ &=& \overbrace {2 \cdot \hat y \cdot \cos \left( {\pi \cdot {f_{{\rm{Schwebung}}}} \cdot t} \right)}^{{\rm{Amplitudenfaktor}}} \cdot \sin \left( {2 \cdot \pi \cdot \underbrace {\frac{{{f_1} + {f_2}}}{2}}_{{f_{\rm{R}}}} \cdot t} \right)\end{eqnarray}\]
Hörbeispiele
So hört sich der Ton mit \(f_1=530\,\rm{Hz}\) an:
So hört sich der Ton mit \(f_2=500\,\rm{Hz}\) an:
So hört sich die sich ergebende Schwebung mit Ergeb Ton mit \(f_{\rm{Schwebung}}=30\,\rm{Hz}\) an:
Hinweis: Mit dem Computer oder zwei Smartphones kannst du selbst schnell und einfach beliebige Schwebungen erzeugen. Dazu musst du lediglich zwei Sinustöne erzeugen, deren Frequenz sich nicht zu stark voneinander unterscheidet. Am PC geht dies einfach mit Audacity, am Smartphone funktioniert die App phyphox sehr gut.
Anwendungen
•Tiefe Töne sind über große Entfernungen weiter hörbar als hohe Töne. Deswegen versucht man Schiffsbrüchigen eine Pfeife mitzugeben, die möglichst tiefe Töne von sich gibt. Wollte man einen tiefen Ton direkt erzeugen, würde die Pfeife (vgl. Orgelpfeife) sehr unhandlich groß. Durch Überlagerung zweier Töne gelingt es eine niederfrequente Schwingung mit der Schwebungsfrequenz zu erzeugen.
•Beim Stimmen einer Gitarre kann man die Schwebung ausnutzen (vgl. die entsprechende Musteraufgabe).