DOPPLER-Effekt beim Krankenwagen
Du hast sicher schon erlebt, dass sich eine Schallquelle auf dich zu bewegt hat (z.B. Krankenauto mit Sirene), bzw. dass du dich mit höherer Geschwindigkeit einer ruhenden Schallquelle genähert hast. In beiden Fällen tritt eine Frequenzänderung des gehörten Tones auf.
Dieses Phänomen, das in ähnlicher Form auch bei bewegten Lichtquellen auftritt, wurde von dem österreichischen Physiker Christian DOPPLER (1803 – 1853) geklärt. Man nennt dieses Phänomen seither den DOPPLER-Effekt.
Die folgende Simulation in Abb. 1 zeigt einen Notarztwagen, der mit eingeschaltetem Martinshorn an einer Person vorbeifährt, die an der Straße steht. Solange das Fahrzeug näherkommt, nimmt die Person einen höheren Ton wahr (entsprechend einer höheren Frequenz). Später, wenn sich das Fahrzeug wieder entfernt, hört sie einen niedrigeren Ton (niedrigere Frequenz).
Bemerkung: In einer Hinsicht ist diese App ausgesprochen unrealistisch: Damit der DOPPLER-Effekt deutlich zu erkennen ist, wurde eine extrem hohe Fahrzeuggeschwindigkeit (60 % der Schallgeschwindigkeit) vorausgesetzt.
Wir danken Herrn Walter Fendt für die Erlaubnis, diese HTML5/Javascript-Animation auf LEIFIphysik zu nutzen.
Aufgabe
Bestimme durch Stoppen mit der Stoppuhr den zeitlichen Abstand zwischen zwei Wellenfronten beim sich nähernden und beim sich entfernenden Krankenwagen.
Errechne daraus und aus der Schallgeschwindigkeit \({c_{Schall}} = 334\frac{{\rm{m}}}{{\rm{s}}}\) jeweils die (unrealistische) Frequenz.
Detaillierte Simulation
Noch etwas detaillierter kannst du dir den DOPPLER-Effekt anhand der folgenden Simulation studieren. Die Schallgeschwindigkeit beträgt hier \(300\rm{\frac{m}{s}}\). Du kannst hierbei einige der relevanten Parameter variieren und die sich dadurch ergebenden Änderungen einprägen. Insbesondere können auch die Fälle untersucht werden, bei denen die Quellengeschwindigkeit größer als die Schallgeschwindigkeit ist (Überschallgeschwindigkeit).
Bei der Analyse des DOPPLER-Effektes muss man drei verschiedene Fälle unterscheiden.
1. Fall: Der Sender bewegt sich – der Empfänger ruht (in Bezug zum Medium)
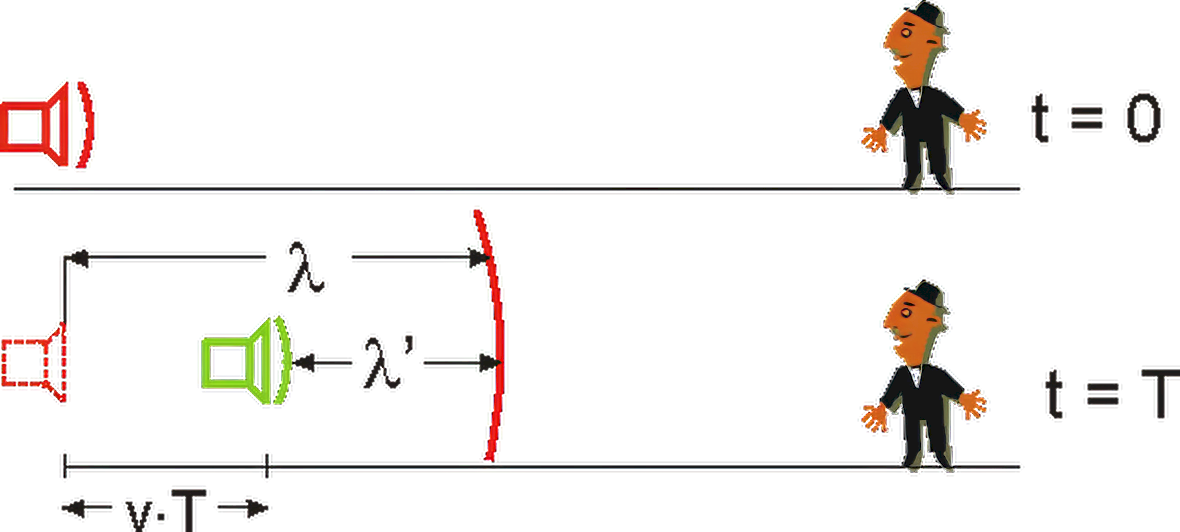
In einem Medium mit der Ausbreitungsgeschwindigkeit \(c\) bewegt sich ein Sender mit der Geschwindigkeit \(v_{\rm{S}}\) auf einen ruhenden Empfänger zu. Der Sender sendet dabei eine Welle mit der Frequenz \(f\) bzw. der Wellenlänge \(\lambda\) aus.
Der Empfänger beobachtet eine Welle, die mit der Ausbreitungsgeschwindigkeit \(c\) bei ihm ankommt, aber eine kleinere Wellenlänge \(\lambda '\) besitzt.
Wir betrachten dazu Abb. 3: Bei \(t=0\) sende der Sender gerade einen Wellenberg (rot) ab. Zur Zeit \(t=T\) hat sich dieser Wellenberg um die Strecke \(\lambda\) ausgebreitet. Die Quelle (jetzt grün) hat sich in dieser Zeit um die Strecke \(v_{\rm{S}} \cdot T\) bewegt und sendet gerade wieder einen Wellenberg (grün) aus.
Für die beim Empfänger registrierte Wellenlänge \(\lambda '\) gilt\[\lambda ' = \lambda - v_{\rm{S}} \cdot T < \lambda\]Für die beim Empfänger registrierte Frequenz \(f'\) gilt dann\[f' = \frac{c}{{\lambda '}} = \frac{c}{{\lambda - v_{\rm{S}} \cdot T}} = \frac{c}{{\frac{c}{f} - v_{\rm{S}} \cdot T}}\]Erweitern des Bruches mit \(f\) ergibt\[f' = f \cdot \frac{c}{{c - v_{\rm{S}} \cdot T \cdot f}} = f \cdot \frac{c}{{c - v_{\rm{S}} \cdot T \cdot \frac{1}{T}}} = f \cdot \frac{c}{{c - v_{\rm{S}}}} > f \quad (1)\]Die Frequenz wird also – wie die Erfahrung auch zeigt – größer.
Bewegt sich der Sender vom Empfänger weg, müssen wir in obiger Formel nur \(v_{\rm{S}}\) durch \((-v_{\rm{S}})\) ersetzen. Für die beim Empfänger registrierte Wellenlänge \(\lambda '\) gilt dann\[\lambda ' = \lambda + v_{\rm{S}} \cdot T > \lambda\]Für die beim Empfänger registrierte Frequenz \(f'\) gilt schließlich\[f' = f \cdot \frac{c}{{c + v_{\rm{S}}}} < f \quad (2)\]Die Frequenz wird also – wie die Erfahrung auch zeigt – kleiner.
DOPPLER-Effekt - Bewegter Sender - ruhender Empfänger
In einem Medium mit der Ausbreitungsgeschwindigkeit \(c\) bewegt sich ein Sender mit der Geschwindigkeit \(v_{\rm{S}}\) und sendet dabei eine Welle mit der Frequenz \(f\) aus. Die ausgesendete Welle trifft auf einen Empfänger, der in dem Medium ruht. Durch die Relativbewegung des Senders zum Medium ändert sich für den Empfänger die Wellenlänge der Welle.
Bewegt sich der Sender auf den Empfänger zu, so steigt die Frequenz \(f'\), mit der der Empfänger die Welle empfängt, gemäß\[f' = f \cdot \frac{c}{{c - v_{\rm{S}}}} \quad (1)\]Bewegt sich der Sender vom Empfänger weg, so sinkt die Frequenz \(f'\), mit der der Empfänger die Welle empfängt, gemäß\[f' = f \cdot \frac{c}{{c + v_{\rm{S}}}} \quad (2)\]
2. Fall: Der Sender ruht (in Bezug zum Medium) – der Empfänger bewegt sich
In einem Medium mit der Ausbreitungsgeschwindigkeit \(c\) ruht ein Sender. Der Sender sendet eine Welle mit der Frequenz \(f\) bzw. der Wellenlänge \(\lambda\) aus. Ein Empfänger bewegt sich mit der Geschwindigkeit \(v_{\rm{E}}\) auf den ruhenden Sender zu.
Der Empfänger beobachtet eine Welle, die die Wellenlänge \(\lambda\) besitzt, aber mit der Geschwindigkeit \(c + v_{\rm{E}}\) bei ihm ankommt.
Für die beim Empfänger registrierte Frequenz \(f'\) gilt\[f' = \frac{{c + v_{\rm{E}}}}{\lambda } = \frac{{c + v_{\rm{E}}}}{{\frac{c}{f}}} = f \cdot \frac{{c + v_{\rm{E}}}}{c} > f \quad (3)\]Die Frequenz wird also – wie die Erfahrung auch zeigt – größer. Beachte, dass die Formel \((3)\) nicht mit der Formel \((2)\) übereinstimmt.
Bewegt sich der Empfänger vom Sender weg, müssen wir in obiger Formel nur \(v_{\rm{E}}\) durch \((-v_{\rm{E}})\) ersetzen. Für die beim Empfänger registrierte Frequenz \(f'\) gilt schließlich\[f' = \frac{{c - v_{\rm{E}}}}{\lambda } = \frac{{c - v_{\rm{E}}}}{{\frac{c}{f}}} = f \cdot \frac{{c - v_{\rm{E}}}}{c} < f \quad (4)\]Die Frequenz wird also – wie die Erfahrung auch zeigt – kleiner. Beachte, dass die Formel \((4)\) nicht mit der Formel \((1)\) übereinstimmt.
DOPPLER-Effekt - Ruhender Sender - Bewegter Empfänger
In einem Medium mit der Ausbreitungsgeschwindigkeit \(c\) ruht ein Sender und sendet eine Welle mit der Frequenz \(f\) aus. Die ausgesendete Welle trifft auf einen Empfänger, der sich mit der Geschwindigkeit \(v_{\rm{E}}\) in dem Medium bewegt. Durch die Relativbewegung des Empfängers zum Medium ändert sich für den Empfänger die Ausbreitungsgeschwindigkeit \(c\) der Welle.
Bewegt sich der Empfänger auf den Sender zu, so steigt die Frequenz \(f'\), mit der der Empfänger die Welle empfängt, gemäß\[f' = f \cdot \frac{{c + v_{\rm{E}}}}{c} \quad (3)\]Bewegt sich der Empfänger vom Sender weg, so sinkt die Frequenz \(f'\), mit der der Empfänger die Welle empfängt, gemäß\[f' = f \cdot \frac{{c - v_{\rm{E}}}}{c} \quad (4)\]
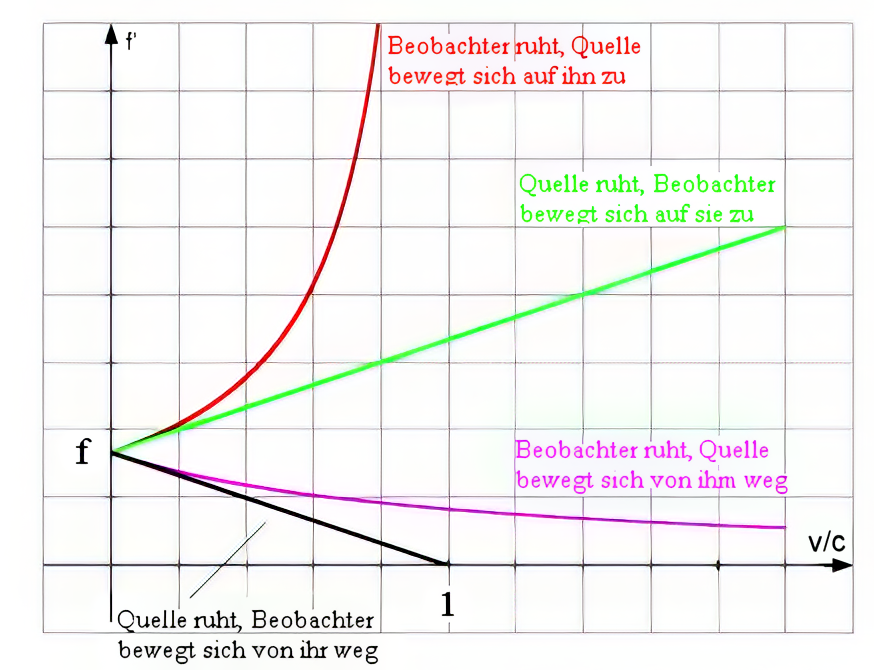
In der graphischen Darstellung ist die Frequenz \(f’\) in Abhängigkeit vom Quotienten \(\frac{v}{c}\) der Geschwindigkeit \(v\) und der Schallgeschwindigkeit \(c\) für die vier verschiedenen Fälle dargestellt.
MACH-Kegel
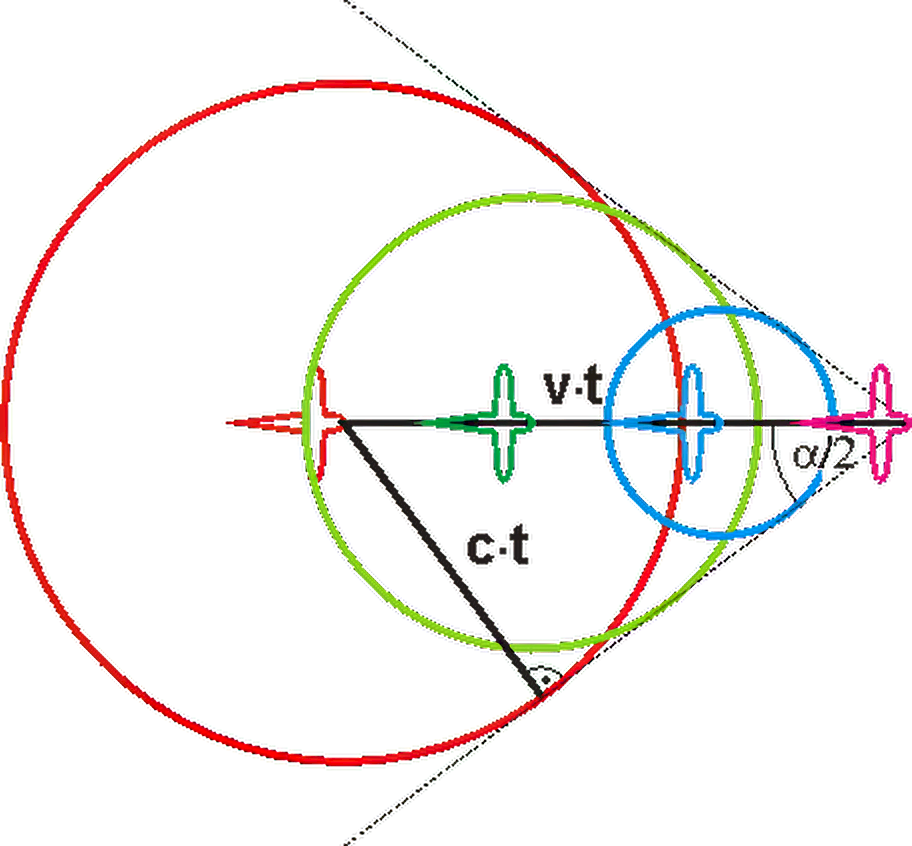
Bewegt sich ein Sender in einem Medium mit einer Geschwindigkeit \(v_{\rm{S}} > c\), so kommt es für zu einer Verdichtung der Wellenfronten. Die Einhüllende der Wellenberge wird nach dem österreichischen Physiker Ernst MACH (1838 - 1916) als MACHscher Kegel bezeichnet. An der Mantelfläche des Kegels summieren sich die Luftverdichtungen, es entsteht ein besonders starker Überdruck, der sich für den Beobachter in einem explosionsartigen Knall äußert. Ein mit Überschall fliegendes Flugzeug "schleppt" seinen "Düsenknall" auf dem Mantel des MACHschen Kegels fortwährend hinter sich her.
Für den Öffnungswinkel des MACHschen Kegels gilt\[\sin \left( {\frac{\alpha }{2}} \right) = \frac{{c \cdot t}}{{v_{\rm{S}} \cdot t}} = \frac{c}{v_{\rm{S}}}\]
Die Abbildung 6 zeigt einen Düsenjet der US-Navy, der gerade die Schallmauer durchbricht. Auf Grund günstiger atmosphärischer Bedingungen ist die Hüllkurve des MACHschen Kegels zu beobachten.