Mit dem SCHÜRHOLZ-Versuch gelingt es auf physikalisch einwandfreie Weise eine Formel für die innere Energie zu entwickeln. Die Versuchsdurchführung und -auswertung ist aber sehr aufwändig. Deshalb sollten sich nur sehr interessierte und leistungsfähige Schüler an das Thema heranwagen.
Aufbau, Durchführung und Beobachtung
Ein Plastikband ist einseitig an einer Federwaage befestigt und um einen drehbaren Aluminiumzylinder mit Radius \(r = 2{,}35\,{\rm{cm}}\) und der Masse \(m = 220\,{\rm{g}}\) gewickelt. Am anderen Ende hängt ein Gewichtsstück. Dreht man den Aluminiumzylinder nicht, so wird das Gewichtsstück nur durch die Federwaage gehalten. Dreht man dagegen an der Kurbel, so wirkt eine Reibungskraft auf das Plastikband nach oben, so dass das Gewichtsstück durch die Summe aus Reibungskraft und Federkraft im Gleichgewicht gehalten wird.
| Aufgabe | ||
|
a) |
Berechne den Betrag \({F_{\rm{R}}}\) der Reibungskraft. |
|
|
b) |
Berechne die Streckenlänge \(s\), den die Zylinderoberfläche bei einer Umdrehung gegenüber dem Seilstück zurücklegt. |
|
|
c) |
Berechne die mechanische Reibungsarbeit \({W_{\rm{R,1}}}\), die bei einer Umdrehung geleistet wird. |
|
Die mechanische Arbeit \({W_{\rm{R}}}\) führt nun zur Erhöhung \(\Delta {E_{\rm{i}}}\) der inneren Energie des Zylinders (und von Schnur und Umgebung). Da das Kunststoffband wenig Energie aufnimmt können wir näherungsweise davon ausgehen, dass die mechanische Arbeit fast ausschließlich zur Erhöhung der inneren Energie des Zylinders dient. Es gilt also \(\Delta {E_{\rm{i}}} = {W_{\rm{R}}}\).
Nun soll in mehreren Versuchsreihen erkundet werden, wie die Änderung der inneren Energie eines Festkörper von dessen physikalischen Eigenschaften abhängt.
| Versuchsreihe 1: Zusammenhang zwischen \(\Delta {E_{\rm{i}}}\) und der Temperaturänderung \(\Delta \vartheta \) | ||||||||||||||||
|
An dem Aluminiumzylinder (\(r = 2,35{\rm{cm}}\), \(m = 220{\rm{g}}\)) wird mit der oben berechneten Reibungskraft \({F_{\rm{R}}} = 8{\rm{N}}\) gekurbelt. Gemessen wird die Temperatur \(\vartheta \) des Zylinders in Abhängigkeit von der Zahl \(N\) der Umdrehungen. Dabei ergaben sich folgende Werte:
|
 |
|||||||||||||||
|
a) |
Entwickle den Zusammenhang zwischen der Anzahl \(N\) der Umdrehungen des Zylinders und der dadurch verursachten Erhöhung \(\Delta {E_{\rm{i}}}\) der inneren Energie des Zylinders. Ergänze die Tabelle um eine weitere Zeile, in die die Energieerhöhungen eingetragen werden können, beschrifte diese Zeile korrekt, berechne die zu den jeweiligen Umdrehungszahlen gehörenden Energieerhöhungen und trage die berechneten Werte in die Tabelle ein. |
|||||||||||||||
|
b) |
Ergänze die Tabelle um eine weitere Zeile, in die die Temperaturerhöhungen \(\Delta \vartheta \) eingetragen werden können, beschrifte diese Zeile korrekt, berechne die zu den jeweiligen Temperaturen gehörenden Temperaturerhöhungen in Bezug zur Anfangstemperatur und trage die berechneten Werte in die Tabelle ein. |
|||||||||||||||
|
c) |
Erstelle ein \(\Delta \vartheta \)-\(\Delta {E_{\rm{i}}}\)-Diagramm und interpretiere den sich ergebenden Graphen. |
|||||||||||||||
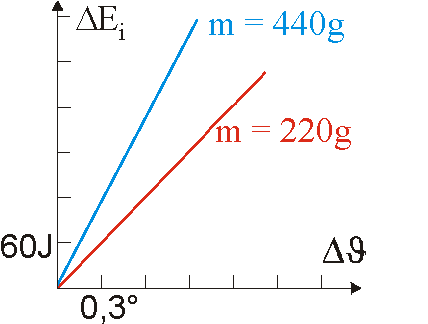
| Versuchsreihe 2: Zusammenhang zwischen \(\Delta {E_{\rm{i}}}\) und der Masse \(m\) | ||||||||||||
|
Nun wird der Aluminiumzylinder durch einen anderen mit doppelter Masse (\(m = 440{\rm{g}}\)) ausgetauscht und wieder mit der oben berechneten Reibungskraft \({F_{\rm{R}}} = 8{\rm{N}}\) gekurbelt. Gemessen wird wieder die Temperatur \(\vartheta \) des Zylinders in Abhängigkeit von der Zahl \(N\) der Umdrehungen. Dabei ergaben sich folgende Werte:
|
 |
|||||||||||
|
a)
|
Werte den Versuch analog zu Versuchsreihe 1 aus und vergleiche den entstehenden Graphen mit dem aus Versuchsreihe 1. |
|||||||||||
|
b) |
Fasse die Ergebnisse der Versuchsreihen 1 und 2 zusammen. |
|||||||||||
|
Als Ergebnis der beiden Versuchsreihen erhält man |
|
Aufgabe: Bestimmung der spezifischen Wärmekapazität von Aluminium Bestimme aus den Versuchsdaten die spezifische Wärmekapazität von Aluminium. |
|
Aufgabe: Bestimmung der spezifischen Wärmekapazität von Kupfer Der gleiche Versuch wird nun mit einem Kupferzylinder von \(m = 660{\rm{g}}\) durchgeführt. Dabei ergab sich bei \(N=250\) Umdrehungen, d.h. einer Energiezufuhr von \(\Delta {E_{\rm{i}}} = 300{\rm{J}}\), eine Erwärmung von \(1,2{\rm{^\circ C}}\). Berechne die spezifische Wärmekapazität von Kupfer und vergleiche sie mit der von Aluminium. |


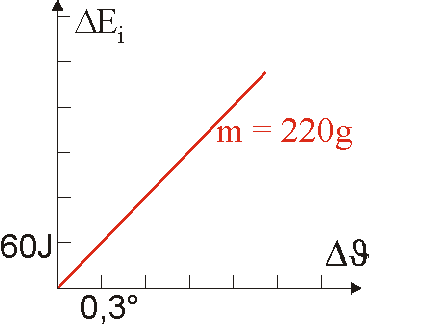 Zum einen sieht man direkt, dass der Graph eine Ursprungsgerade ist. Zum anderen konnte man bereits an der Wertetabelle erkennen, dass sich für die gleiche Erhöhung \(\Delta {E_{\rm{i}}}\) der inneren Energie (pro 50 Umdrehungen werden \(60\rm{J}\) zugeführt) immer die gleiche Temperaturerhöhung \(\Delta \vartheta \) (\(0,3{\rm{^\circ C}}\)) ergibt.
Zum einen sieht man direkt, dass der Graph eine Ursprungsgerade ist. Zum anderen konnte man bereits an der Wertetabelle erkennen, dass sich für die gleiche Erhöhung \(\Delta {E_{\rm{i}}}\) der inneren Energie (pro 50 Umdrehungen werden \(60\rm{J}\) zugeführt) immer die gleiche Temperaturerhöhung \(\Delta \vartheta \) (\(0,3{\rm{^\circ C}}\)) ergibt.