Nach der bekannten EINSTEINschen Energie-Masse-Beziehung kann man dem Photon der Energie \(h \cdot f\) eine Masse zuordnen. Es gilt\[ E=m_{\rm{Ph}} \cdot c^2 \Rightarrow h \cdot f = m_{\rm{Ph}} \cdot c^2 \Rightarrow m_{\rm{Ph}} = \frac{h \cdot f}{c^2} \]Wenn Photonen eine Masse haben, so müssen sie auch durch Gravitationsfelder beeinflussbar sein. Insbesondere bei der Passage am Sonnenrand sollte eine Ablenkung des Lichtes eventuell beobachtbar sein.
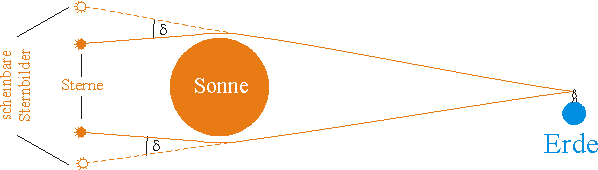
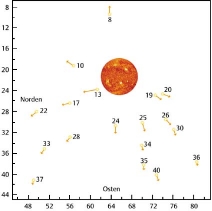
| Sterne, die dicht neben der Sonne stehen (vgl. Skizze oben), sind im Normalfall nicht zu beobachten, da die Sonnenhelligkeit alles überstrahlt. Wenn allerdings eine Sonnenfinsternis herrscht, können diese Sterne fotographiert werden. Das von ihnen ausgehende Licht wird nach EINSTEIN von der Sonne abgelenkt. Für einen Erdbeobachter würden die Sternbilder nach außen verschoben erscheinen. Legt man nun ein Sternbild, das während einer Sonnenfinsternis gewonnen wurde über ein Bild, welches das gleiche Sternenfeld bei Nacht zeigt, so stellt man Verschiebungen fest, wie sie in der nebenstehenden Abbildung durch Striche dargestellt sind. |
|
Die durch die Relativitätstheorie EINSTEINs vorhergesagte Ablenkung des Lichtstrahls von \(\delta = 1{,}25''\)(Winkelsekunden) konnte durch die Messung der Ablenkung des Lichtstrahls, der am Sonnenrand entlang streift, nicht exakt bestätigt werden. Die Messergebnisse lagen im Bereich von \(\delta = 1{,}5''\) bis \(\delta = 2{,}2''\). In jüngerer Zeit gelang es jedoch durch die Beobachtung der Ablenkung der Radiostrahlung eines Quasars EINSTEINs Vorhersage bis auf einen Fehler von \(3\%\) zu bestätigen.
Die Idee für die Überprüfung der vorhergesagten Lichtablenkung an der Sonne stammt übrigens von EINSTEIN selbst. Über die Beobachtung der Sonnenfinsternis im Jahre 1919 berichtet die Neue Züricher Zeitung in einem lesenswerten Artikel.
Hinweis: Die Weite \(\delta \) des Ablenkwinkels kann schon mit den Mitteln der NEWTONschen Mechanik unter vereinfachenden Annahmen ausgerechnet werden. Allerdings ist das Ergebnis nur halb so groß wie dasjenige, welches mit Hilfe der allgemeinen Relativitätstheorie berechnet werden kann. Beachte dazu die entsprechende Musteraufgabe.
Bestätigung durch ein "irdisches" Experiment
Den Physikern Robert POUND (1919 - 2010) und Glen REBKA (1931 - 2015) gelang im Jahre 1960 durch das POUND-REBKA-Experiment eine Bestätigung der Vorhersage von EINSTEIN einer Photonenmasse in einem "irdischen" Experiment.
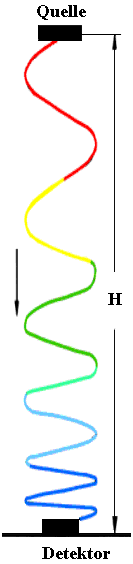
In 1960, R. POUND and G. REBKA, Jr. at Harvard University conducted experiments in which photons (gamma rays) emitted at the top of a 22.57 m high apparatus were absorbed at the bottom, and photons emitted at the bottom of the apparatus were absorbed at the top. The experiment showed that photons which had been emitted at the top had a higher frequency upon reaching the bottom than the photons which were emitted at the bottom. And photons which were emitted at the bottom had a lower frequency upon reaching the top than the photons emitted at the top. These results are an important part of the experimental evidence supporting general relativity theory which predicts the observed "redshifts" and "blueshifts."
Hinweise
Die dargestellten Vorstellungshilfen (Teilchen- und Wellenbild) treffen nicht die Realität der Versuchsdurchführung. REBKA und POUND arbeiteten mit einer Gammastrahlungsquelle und nicht mit sichtbarem Licht.
Beachte, dass die Quanten im Gravitationsfeld nicht schneller, sondern energiereicher werden, was sich in einer Frequenzerhöhung äußert.
Berechnung der Frequenzverschiebung

Es wird die Bewegung des Photons von oben nach unten betrachtet (Blauverschiebung): Die Zunahme der Quantenenergie ist gleich dem Verlust an potenzieller Energie. Damit ergibt sich\[{h \cdot \Delta f = {m_{{\rm{Ph}}}} \cdot g \cdot H = \frac{{h \cdot f}}{{{c^2}}} \cdot g \cdot H}\]und weiter\[{\frac{{\Delta f}}{f} = \frac{{g \cdot H}}{{{c^2}}}}\]Einsetzen der gegebenen Werte liefert\[{\frac{{\Delta f}}{f} = \frac{{9{,}81\,\frac{{\rm{m}}}{{{{\rm{s}}^2}}} \cdot 22{,}57\,{\rm{m}}}}{{{{\left( {3 \cdot 10^8\,\frac{{\rm{m}}}{{\rm{s}}}} \right)}^2}}} = 2{,}5 \cdot 10^{-15}}\]Aus dem Ergebnis sieht man, dass die relative Frequenzzunahme extrem klein ist. Benutzt man aber einen Sender, der Gammastrahlung emittiert, so ist es möglich, diese Frequenzzunahme mit Hilfe des MÖSSBAUER1-Effekts experimentell nachzuweisen. Der von POUND und REBKA gemessene Wert für die Frequenzverschiebung stimmte mit der oben berechneten Frequenzverschiebung sehr gut überein. Somit bestätigt dieser Versuch, dass man Photonen eine Masse zuordnen kann.
1 Rudolf MÖSSBAUER (1929 - 2011), Nobelpreisträger der Physik (1961) aus München