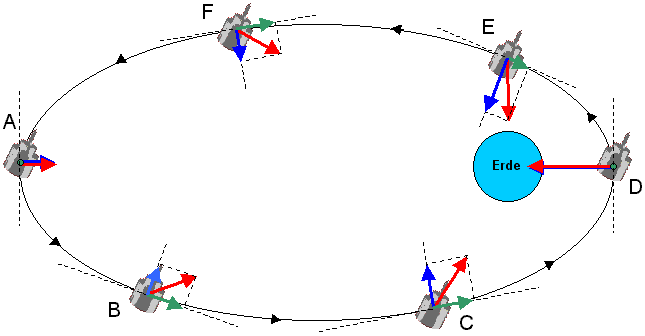
Auch für künstliche Erdsatelliten gilt das 1. KEPLERsche Gesetz; sie bewegen sich auf Ellipsenbahnen um die Erde. Die Erde steht in einem Brennpunkt dieser Ellipsen. In der folgenden Abbildung ist für verschiedene Bahnpositionen die Gravitationskraft eingezeichnet (rote Pfeile!). Wegen der unterschiedlichen Entfernungen zur Erde ist ihr Betrag verschieden groß.
Fertige eine Skizze der oben dargestellten Bahn an. Zeichne in den Punkten A bis F die Tangenten an die Bahnkurve. Zerlege die Gravitationskraft an den verschiedenen Stellen in die beiden Komponenten parallel und senkrecht zur Tangente.
Erläutere, welche der beiden Kraftkomponenten den Betrag und welche die Richtung der Satellitengeschwindigkeit ändert. Erläutere weiter, auf welcher Strecke der Satellit schneller, auf welcher er langsamer wird.
Begründe, warum eine kleine Kraft im erdfernsten Punkt genau die gleiche Bahnkrümmung bewirkt wie eine viel größere im erdnächsten Punkt.
Die potentielle Energie eines Satelliten der Masse \(m\), der sich im Abstand \(r\) vom Erdmittelpunkt befindet, beträgt
\[{E_{{\rm{pot}}}}(r) =-G \cdot m \cdot M \cdot \frac{1}{r}\]
Dabei steht \(M\) für die Masse der Erde. Anmerkung: Die Physiker haben vereinbart das Nullniveau der potentiellen Energie so zu legen, dass nur negative Werte auftreten. Damit wird zum Ausdruck gebracht, dass ein Körper im Gravitationsfeld nicht frei ist. Ein Körper, der unendlich weit von der Erde entfernt ist , der also durch keine Gravitationskraft mehr an die Erde gebunden ist, wird als frei bezeichnet und hat die potentielle Energie null. Damit folgt für die Gesamtenergie des Satelliten
\[{E_{{\rm{ges}}}} = {E_{{\rm{kin}}}} + {E_{{\rm{pot}}}} = \frac{1}{2} \cdot m \cdot {v^2} - G \cdot m \cdot M \cdot \frac{1}{r}\]
Zunächst soll nun ein Satellit auf einer Kreisbahn betrachtet werden.
Die Gravitationskraft liefert die für die Kreisbahn erforderliche Zentripetalkraft. Leite aus diesem Kraftansatz eine Formel für die Satellitengeschwindigkeit \(v\) in Abhängigkeit von \(r\) her.
Berechne die kinetische Energie des Satelliten. Leite hierzu eine Formel in Abhängigkeit von \(r\) her und vergleiche das Ergebnis mit der potentiellen Energie.
Berechne die Gesamtenergie des Satelliten. Leite hierzu eine Formel in Abhängigkeit von \(r\) her und vergleiche das Ergebnis wieder mit der potentiellen Energie.
Aus diesen Energiegleichungen liest man ab: Soll der Satellit auf eine höhere Bahn gehoben werden, muss ihm Energie zugeführt werden, z.B. durch Zünden einer Rakete. Dadurch erfährt der Satellit den erforderlichen Geschwindigkeitsschub. Auf einer höheren Bahn ist dann zwar seine kinetische Energie geringer als vorher (auf höheren Bahnen ist die Geschwindigkeit kleiner!), dafür erhöht sich aber die potentielle Energie.
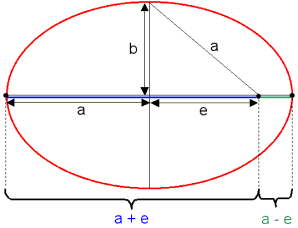
Nun soll ein Satellit auf der Ellipsenbahn betrachtet werden. Die Bezeichnungen bei der Geometrie der Ellipse sind üblicherweise \(a\): große Halbachse, \(b\): kleine Halbachse und \(e\): lineare Exzentrizität.
Auf der Ellipsenbahn schwankt der Radius \(r\) (Entfernung: Erdmittelpunkt - Satellit) zwischen den Werten \(a + e\) (im erdfernsten Punkt) und \(a - e\) (im erdnächsten Punkt). Entsprechend ändert sich die kinetische und die potentielle Energie des Satelliten für die im letzten Abschnitt die Formeln
\[{E_{{\rm{kin}}}} = \frac{1}{2} \cdot G \cdot \frac{{m \cdot M}}{r}\]
und
\[{E_{{\rm{pot}}}} =-G \cdot \frac{{m \cdot M}}{r}\]
hergeleitet wurde. Über die gesamte Bahn gemittelt ist der Radius \(r\) gleich der großen Halbachse \(a\). Damit ergibt sich für die Gesamtenergie des Satelliten auf der Ellipsenbahn
\[{E_{{\rm{ges}}}} = {E_{{\rm{kin}}}} + {E_{{\rm{pot}}}} = \frac{1}{2} \cdot G \cdot \frac{{m \cdot M}}{a} - G \cdot \frac{{m \cdot M}}{a} =-\frac{1}{2} \cdot G \cdot \frac{{m \cdot M}}{a}\]
Im Abstand \(r\) vom Erdmittelpunkt befindet sich ein Satellit auf einer Ellipsenbahn um die Erde mit der großen Halbachse \(a\). Berechne die Geschwindigkeit des Satelliten in dieser Position.