Halbwertszeit einer Probe mit vielen radioaktiven Kernen
Wann ein einzelner Kern in einem radioaktiven Präparat zerfällt, kann nicht vorhergesagt werden. Hat man aber viele noch unzerfallene, radioaktive Kerne vorliegen, so kann man Aussagen über den Verlauf des Zerfalls für die Gesamtheit der Kerne machen. In der Animation wird dies am Beispiel des β--Zerfalls von Fluor-20 dargestellt.
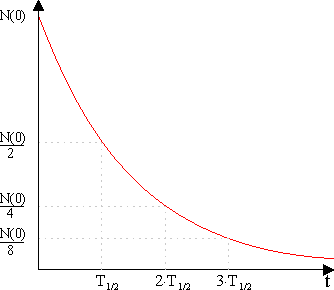
Der zeitliche Verlauf des Zerfalls einer bestimmten radioaktiven Substanz ist weder durch starke Felder noch durch Erwärmung oder irgendwelche andere Maßnahmen zu beeinflussen. Unabhängig von der Zahl der Ausgangskerne ist nach einer Halbwertszeit \(T_{1/2}\) die Hälfte (50%), nach der Zeit \(2\cdot T_{1/2}\) ein Viertel (25%), nach der Zeit \(3\cdot T_{1/2}\) ein Achtel (12,5%) der ursprünglich unzerfallenen Kerne vorhanden.
In der Physik nutzt man zeitlich immer gleichartig ablaufende Vorgänge als Uhr. So verwendet man die Schwingungsdauer eines Pendels oder eines Schwingquarzes zum Bau von Uhren. Den zeitlich stets gleich ablaufenden Zerfall radioaktiver Kerne kann man auch für Zeitbestimmungen verwenden wie z.B. die Radiocarbon-Methode zur Altersbestimmung zeigt.
Zeitlicher Verlauf des Zerfalls
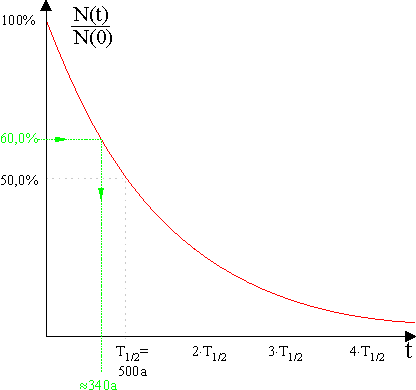
Kennt man den zeitlichen Verlauf des Zerfalls einer Substanz, so kann man mit Hilfe des Prozentsatzes \(\frac{{N(t)}}{{N(0)}} \cdot 100\% \) der zu einem Zeitpunkt \(t\) noch unzerfallenen Kerne die Zeit seit Beginn des Zerfalls bestimmen.
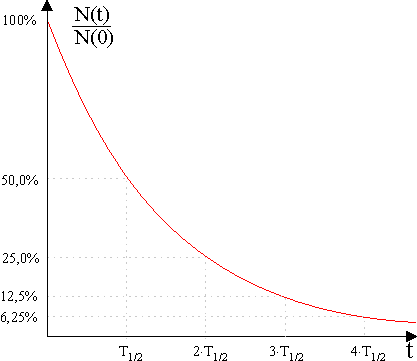
In einer Probe mit der Halbwertszeit \(500\,{\rm{a}}\) waren zu Zerfallsbeginn \(1{,}0\cdot 10^{\rm{3}}\) unzerfallene Kerne. Zum jetzigen Zeitpunkt sind noch \(6{,}0 \cdot 10^{2}\) unzerfallene Kerne in der Probe.
Bestimme graphisch die Zeit, die ungefähr seit Zerfallsbeginn verstrichen ist.
Zeitlicher Verlauf der Aktivität
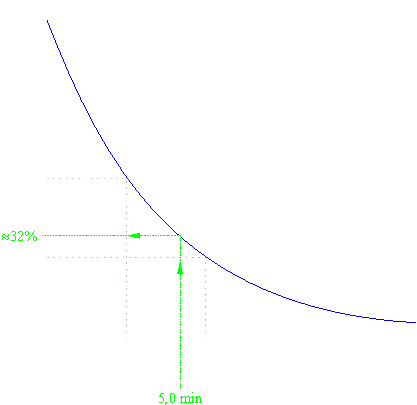
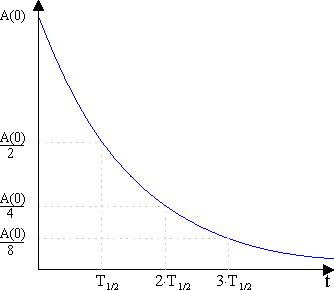
Die Aktivität A (Zahl der Zerfälle pro Zeiteinheit) ist proportional zur Zahl der vorhandenen noch unzerfallenen Kerne \(N(t)\) in einer Probe. Daher gilt auch für den zeitlichen Verlauf der Aktivität einer Probe eine analoge Gesetzmäßigkeit wie für die Zahl der noch unzerfallenen Kerne. Kennt man die Aktivität \(A(0)\) einer Probe zu Beginn eines Zerfalls und die aktuelle Aktivität \(A(t)\), so bestimmt man das Verhältnis \(\frac{{A(t)}}{{A(0)}} \cdot 100\% \) und liest aus der folgenden Kurve die Zeit ab, die seit Beginn des Zerfalls verstrichen ist.
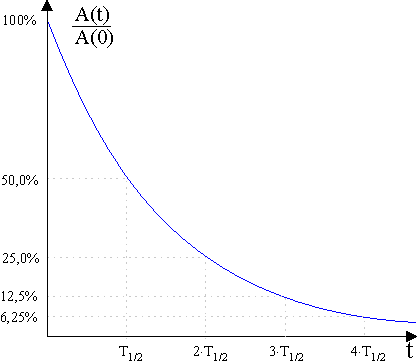
Eine Probe hat die Halbwertzeit von \(3{,}0\min \). Zum Zeitpunkt \(t = 0\) stellt mit einem Zählrohr die Impulsrate \(400\,\frac{{{\rm{Imp}}}}{{\rm{s}}}\) fest.
Bestimme graphisch die Impulsrate, die bei gleicher Anordnung von Zählrohr und Präparat nach \(5{,}0\min \) zu erwarten ist.
Halbwertszeiten verschiedener Isotope
Die Halbwertszeiten radioaktiver Substanzen streuen in einem weiten Bereich. In der folgenden Tabelle sind Isotope mit extrem kurzen und langen Halbwertszeiten aufgeführt. Darüber hinaus findest du die Halbwertszeiten von Isotopen, die im Unterricht von Bedeutung sind.
|
|
|
Hinweis: Sowohl beim t-N(t)- als auch beim t-A(t)-Diagramm ist es gleichgültig, welchen Zeitpunkt man als Startpunkt wählt. Stets ist die Zahl der unzerfallenen Kerne bzw. die Aktivität nach einer Halbwertszeit auf die Hälfte zurückgegangen.
Rechnerische Behandlung des radioaktiven Zerfalls
|
|
|
||||||||||||||||||||||||||||
|
|
Nun wird \(n\) durch \(t\) und \(T_{1/2}\) ausgedrückt. Der Ausdruck in der letzten Zeile der linken Spalte ergibt:
\[t = n \cdot {T_{1/2}} \Leftrightarrow n = \frac{t}{{{T_{1/2}}}}\]
Während \(n\) bisher eine natürliche Zahl war, wollen wir nun auch positive rationale Zahlen für \(n\) zulassen.
Ersetzt man \(n\) in den allgemeinen Gleichungen für \(N(t)\) bzw. \(A(t)\) in den letzten Zeilen der Tabelle, so ergibt sich:
|
|
Aufgabe
Aufgabe
Eine Probe hat die Halbwertzeit von \(3{,}0\,\rm{min}\). Zum Zeitpunkt \(t=0\) stellt mit einem Zählrohr die Impulsrate \(400\,\frac{{{\rm{Imp}}}}{{\rm{s}}}\) fest. Welche Impulsrate ist - bei gleicher Anordnung von Zählrohr und Präparat nach \(5{,}0\,\rm{min}\) zu erwarten?